Topic Content:
- Converting from other Bases to Base 10
- Locating Place Values of Whole and Decimal Numbers
- Power Expansion and Successive Multiplication Methods
Here, we will learn the methods to convert from other bases to Base 10
Example 1.2.1:
Convert
(i) 7603eight to base 10
(ii) 1101two to base 10
(iii) 5B9twelve to base 10
Solution (i) 7603eight to base 10
a. First Method: (Power Expansion)
Power Expansion entails multiplying out the number base using their base values.
- First, write the place values starting from the right-hand side.
- Write each digit under its place value.
- Multiply each digit by its base raised to the corresponding place value.
(i.e. baseplace value, Note: for this question, it will be 8place value) - Add up the products. The answer will be the decimal number in base ten.

Students often find it difficult to locate the place values. The easiest way is to start from the last digit to the first digit. The last Digit always starts with a 0, the digit that follows a 1, and so on. (0, 1 2, 3, etc)
| 3 | 2 | 1 | 0 |
| 7 | 6 | 0 | 3 |
Write down the base raised to the place value. The number we are converting is 7603eight ∴ it’s in base 8.
| 83 | 82 | 81 | 80 |
| 7 | 6 | 0 | 3 |
Multiply each digit by its base raised to the corresponding place value.
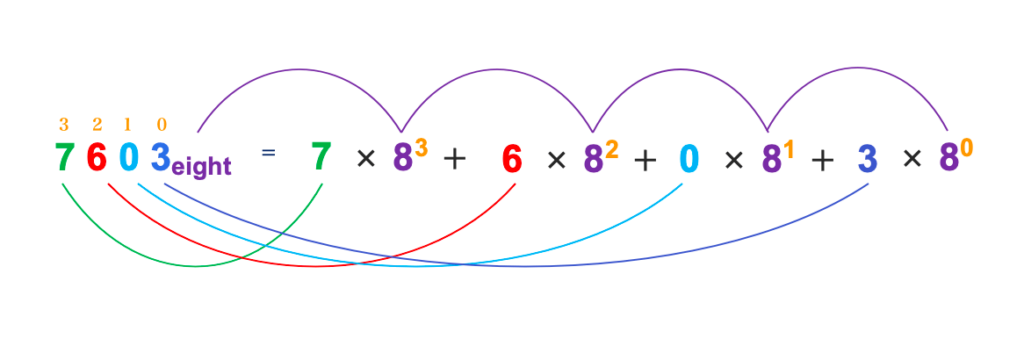
7603eight = (7 × 83) + (6 × 82) + (0 × 81) + (3 × 80)
= 3584 + 384 + 0 + 3
= 3,971ten
∴ 7603eight = 3,971ten
b. Alternate Method – (Successive Multiplication)
7 × 8 = 56 + 6 = 62 × 8 = 496 + 0 = 496 × 8 = 3968 + 3 = 3,971ten
Solution (ii) 1101two to base 10
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Super helpful! First method is so easy, I got confused in class when I was learning this.
Thx
Very helpful
Thanks
Great! and Helpful!!
I love the lesson
This is really Amazing! I couldn’t even believe I’ll fall in love with mathematics, It’s just the understanding and focus. my teacher in school was amazed when I was solving with the Alternative method. Thanks for this great lesson…!!