How To Find Equivalent Fractions

To find an equivalent fraction with a larger numerator and denominator, simply multiply both the numerator and the denominator of the given fraction by the same number. 

For example:

\( \frac {2}{3} = \frac {2}{3}\: \times \: \frac {3}{3}= \frac {6}{9} \)

That is, \( \frac {2}{3}\)is equivalent to \( \frac {6}{9}\)

Worked Example 7.2.1:

Convert \(\frac{2}{9}\) into an equivalent fraction with the denominator 27.  

Solution

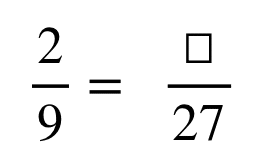
Divide the second denominator by the first denominator to obtain the multiplier.