Back to Course

SS1: CHEMISTRY - 2ND TERM

0% Complete
0/0 Steps
  1. Kinetic Theory of Matter | Week 1
    3 Topics
    |
    1 Quiz
  2. Kinetic Theory of Matter & Gas Laws I | Week 2
    3 Topics
    |
    1 Quiz
  3. Gas Laws II | Week 3
    3 Topics
    |
    1 Quiz
  4. Gas Laws III | Week 4
    3 Topics
    |
    1 Quiz
  5. Gas Laws IV | Week 5
    3 Topics
    |
    1 Quiz
  6. Mole Concept | Week 6
    5 Topics
    |
    1 Quiz
  7. Acid, Bases and Salts I | Week 7
    7 Topics
    |
    1 Quiz
  8. Acid, Bases and Salts II | Week 8
    6 Topics
    |
    2 Quizzes
  9. Acid, Bases and Salts III | Week 9
    3 Topics
    |
    2 Quizzes
  10. Acid, Bases and Salts IV | Week 10
    4 Topics
    |
    1 Quiz
  11. Acid, Bases and Salts V | Week 11
    5 Topics
    |
    1 Quiz

Quizzes




  • Kofa Study
Lesson Progress
0% Complete

Topic Content:

  • Definition of Charles Law
  • Graphical Representation of Charles Law
  • Pictorial Representation of Charles Law
  • How Kinetic Theory Explains Charles Law
  • Calculations Based on Charles Law

A French chemist, Jacques Charles (1746-1823) found the relationship between the volume and temperature under constant pressure.

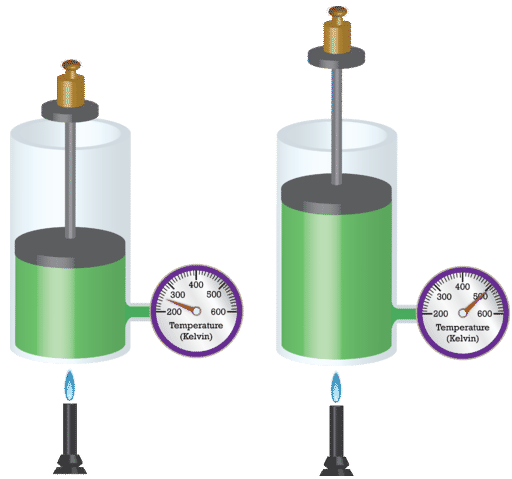
Charles law states that the volume of a given mass of gas is directly proportional to its absolute temperature or temperature in Kelvin, provided pressure remains constant.

It means that the volume of the gas increases as temperature increases and also decreases as temperature decreases i.e. (vice versa).

Charles Law
As a container of a confined gas is heated, its molecules increase in kinetic energy and push the movable piston outward, resulting in an increase in volume.

Mathematically, 

 

You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!

Click on the button "Subscribe Now" below for Full Access!

Subscribe Now

Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!

avataravataravataravatar

Responses

Your email address will not be published. Required fields are marked *

Report

Harassment or bullying behavior
Contains mature or sensitive content
Contains misleading or false information
Contains abusive or derogatory content
Contains spam, fake content or potential malware

Block Member?

Please confirm you want to block this member.

You will no longer be able to:

  • See blocked member's posts
  • Mention this member in posts
  • Invite this member to groups
  • Message this member
  • Add this member as a connection

Please note: This action will also remove this member from your connections and send a report to the site admin. Please allow a few minutes for this process to complete.

Report

You have already reported this .
error: Alert: Content selection is disabled!!