Topic Content:
- Meaning of Lowest Common Multiple (LCM)
- Different Methods of Finding LCM
What is LCM?
The lowest common multiple of two or more numbers is the lowest multiple they have in common.
For example:
The multiples of 2 are 2, 4, 6, 8, 190, 12, 14, 16, 18……
The multiples of 3 are 3, 6, 9, 12, 15, 18 …….
The common multiples of 2 and 3 are 6, 12, 18, ……
The lowest common multiple of 2 and 3 is 6.
Method 1 (Short Division Method):
LCM by division method means finding the least common multiple of a given set of numbers by dividing all the given numbers by a common prime number.
Method 2 (Prime Factorization Method):
Using this method we find the prime factors of the given numbers. We the select each prime factor with the “highest power” and multiply to get the LCM.
Let’s try some examples.
Worked Example 1.4.1:
Find the LCM of:
a. 3, 7 and 10
b. 9 and 15
c. 2 ,3 and 4
d.
23 × 32 × 5
22 × 3 × 5
e.
24 × 32 × 5 × 7 × 112
23 × 5 × 73 × 11
22 × 33 × 5 × 72 × 11
a. 3, 7 and 10
Solution
1st Method (Division Method):
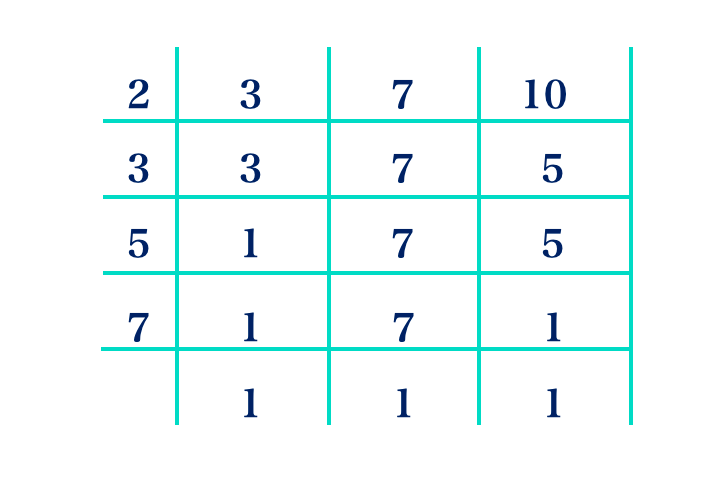
Let us understand this method using the example given below.
Step 1: 2 is the smallest prime number and it is a factor of 10. Write 2 on the left of the three numbers. For each number in the right column, continue calculating out prime numbers which are their factors.
Step 2: 2 divides 10 and the result is 5. But 2 is not a factor of 3 and 7, so we write the number 3 and 7 in the row below as it is.
Step 3: We continue the process until we have only 1’s left
Step 4: Our final step is to multiply the prime numbers on the left. The Least Common Multiple (LCM) is the product of all these prime numbers.
LCM = 2 × 3 × 5 × 7
= 6 × 35
= 210
2nd Method:
Find the prime factors of the given numbers.
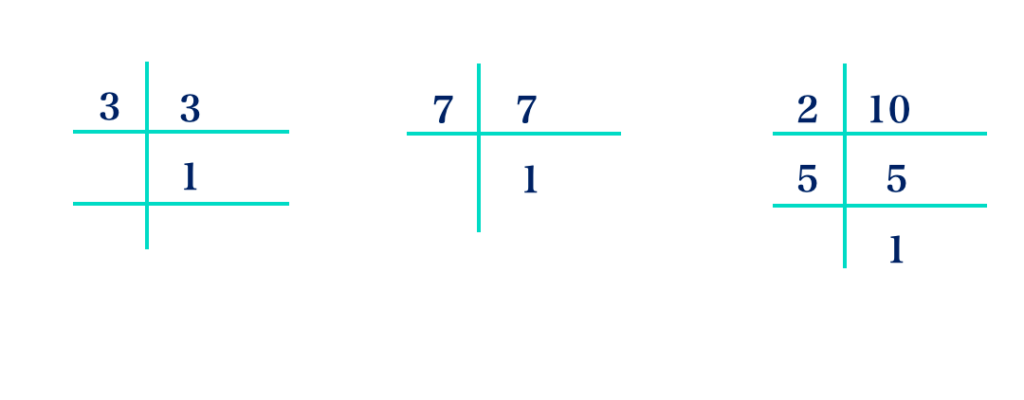
3 = 1 × 3
7 = 1 × 7
10 = 2 × 5
Select each prime factor with the “highest power” and multiply to get the LCM.
∴ L.C.M. = 1 × 2 × 3 × 7 × 5
= 210
b. 9 and 15
Solution
1st Method (Division Method):
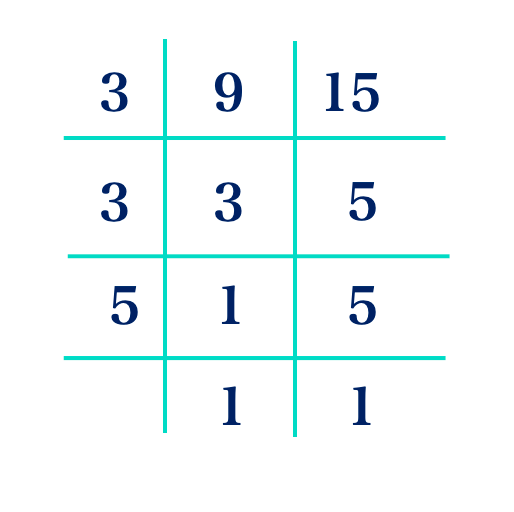
∴ L.C.M. = 3 × 3 × 5
= 9 × 5
= 45
2nd Method (Prime Factorization Method):
Step 1: Resolve each given number into its prime factors and express the factors obtained in exponent form.
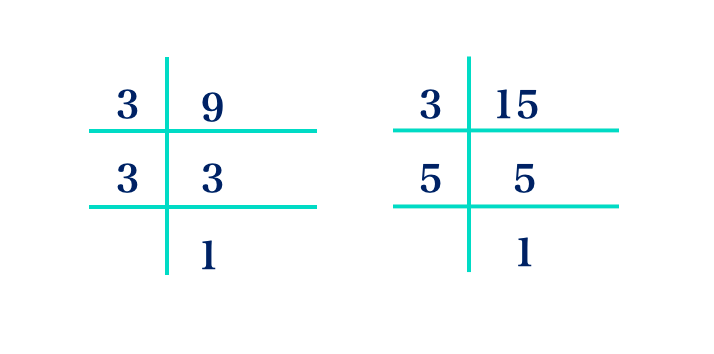
9 = 3 × 3 = 32
15 = 3 × 5
Step 2: Find the product of all the prime factors with highest powers.
= 32 × 5
= 9 × 5
= 45
c. 2, 3 and 4
Solution
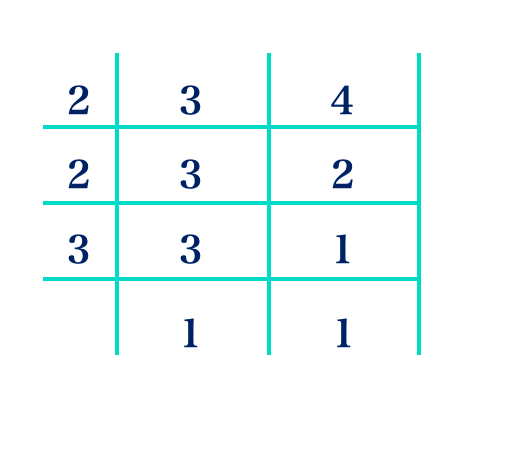
LCM of 3 and 4 = 2 × 2 × 3 = 12
d.
23 × 32 × 5
22 × 3 × 5
Solution
In this case, compare the index (power) of numbers with the same base. The numbers with greater power (index) are the common multiple.
23 × 32 × 5
22 × 3 × 5
= 23 × 32 × 5
LCM = 23 × 32 × 5
e.
24 × 32 × 5 × 7 × 112
23 × 5 × 73 × 11
22 × 33 × 5 × 72 × 112
Solution
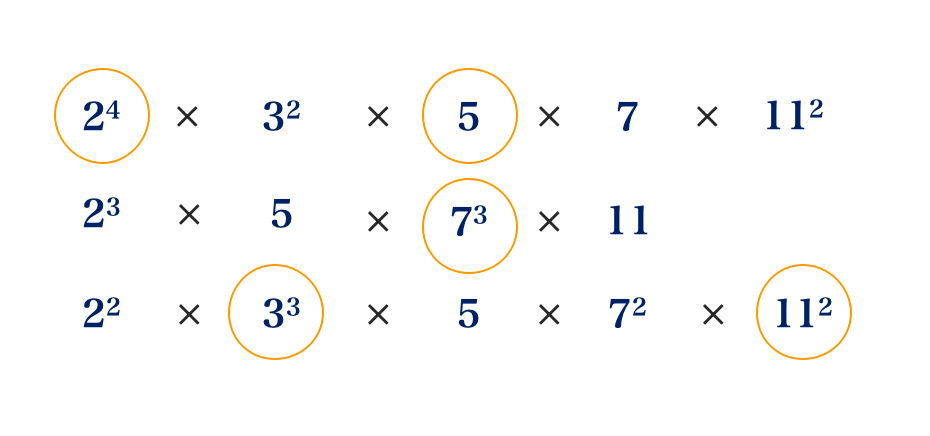
LCM = 24 × 33 × 5 × 73 × 112
Evaluation Questions:
1. Find all the factors of 48
View Answer2. Find the factors of 100 that are
i. Odd numbers
ii. Even numbers
iii. Multiples of 2
iv. Multiples of 5
3. Write down the first six multiples of 7
View Answer4. Express the following numbers as a product of prime factors.
a. 64
b. 120
c. 500
d. 980
5. Express 24 × 36 as a product of its prime factors in index form.
View Answer6. Find the common factors of the following:
a. 16 and 30
b. 36 and 50
7. Find the HCF of:
a. 4 and 12
b. 9, 18 and 54
c. 36 and 81
8. Find the HCF of
a. 22 × 32 × 53 × 7 and 24 × 35 × 5 × 72
b. 52 × 73 and 53 × 74
View Answers9. Find the first three common multiples of
a. 5 and 6
b. 2, 3 and 4
10. Find the LCM of
a. 12, 18 and 36
b. 5, 10, and 15
c. 52 × 7 × 11, 2 × 3 × 5 × 11
d. 23 × 3 × 53; 2 × 32 × 52; 23 × 33 × 5 × 72



Responses