Topic Content:
- Perfect Squares
- Perfect square with a + sign between the two numbers
Perfect square with a negative sign between the two numbers
Worked Examples
- Perfect square with a + sign between the two numbers
A perfect square with a + sign between the two numbers:
(x + a)2 = ( x + a) (x + a)
⇒ x (x + a) + a (x + a)
⇒ x2 + ax + ax + a2
⇒ (x + a)2 = x2 + 2ax + a2
We can state the above result as follows:
The first term squared + twice their product + the square of the second term.
A perfect square with a negative sign between the two numbers:
(x – a)2 = (x – a) (x – a)
⇒ x(x – a) – a (x – a)
⇒ x2 – ax – ax – a2
⇒ x2 – 2ax – a2
⇒ (x – a)2 = x2 – 2ax + a2.
We can state the above result as follows:
the first term squared – twice their product + the square of the second term.
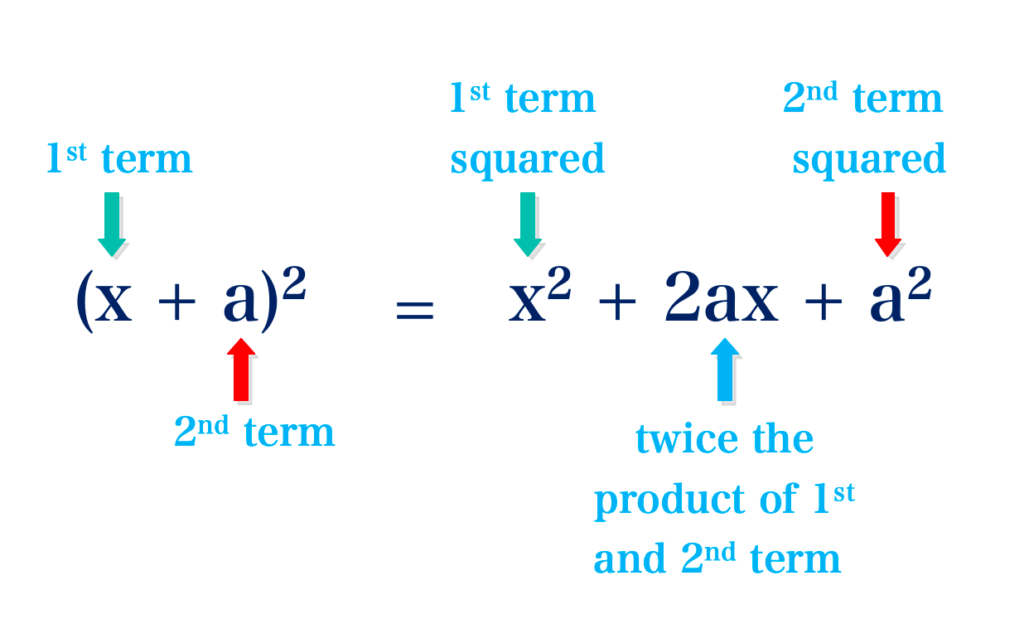
Worked Example 7.1.1:
Write down the expansions of the following:
a. (y + 8)2
b. (y – 5)2
c. (7a – 3)2
d. (2y – 6)2
e. (5x + 4y)2
Solution
a. (y + 8)2
⇒ (y + 8) (y + 8)
⇒ y (y + 8) + 8 (y + 8)
⇒ y2 + 8y + 8y + 64
= y2 + 16y + 64
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses