Factorization of Trinomials of the Form x² + bx + c

A trinomial is an algebraic expression containing three terms.

For example, ax² + b  + c is a trinomial because it has three terms i.e. ax², bx, c  when a = 1 this expression becomes x² + b x  + c,  a simple trinomial.

Some quadratic expression can be factorized by splitting the middle term.

Therefore, to factorize a trinomial of the form ax² + bx + c, look for pairs of factors of the constant term c that adds up to b i.e. the coefficient of x.

Worked Example 6.3.1:

Factorize:

a. x² + 7x  + 10
b. x² + 3x  + 2
c. x² + 8x  + 15
d. y² + 9y + 18
e. 2x² + 13x + 6

Solution

a. x² + 7x  + 10

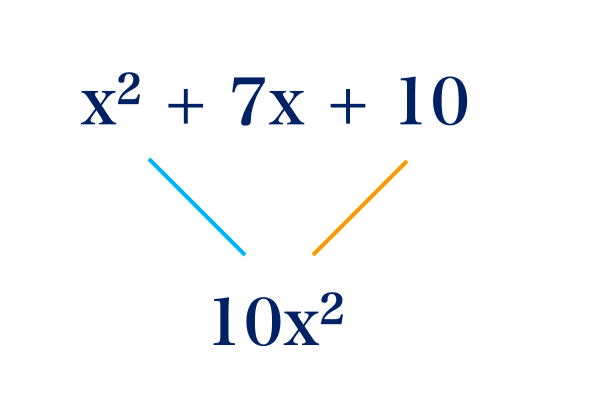
i. First multiply The first and the last term i.e. a × c

ii. Look for the factors of 10x², two factors when they are multiplied give 10x² and when added they give 7x, which is the middle term.

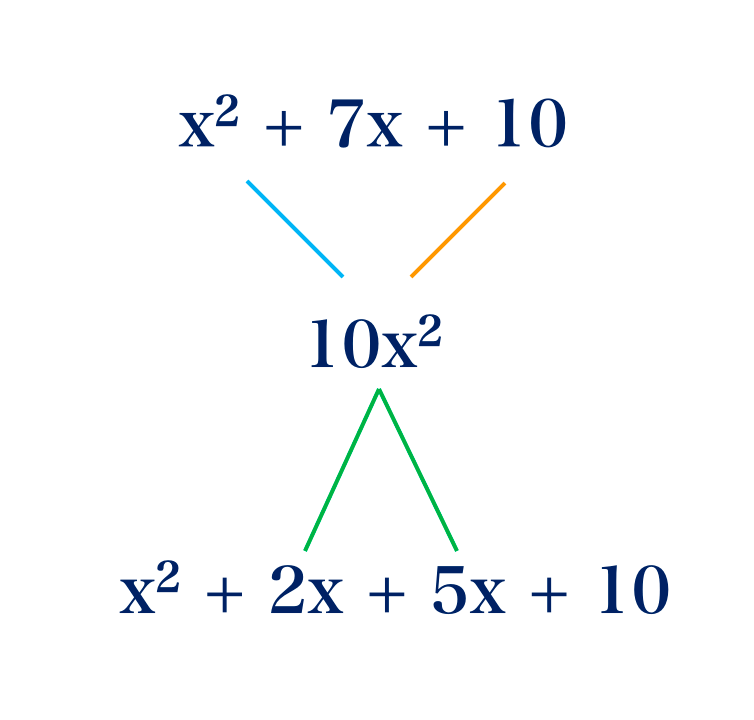
Factors of 10: 1, 2, 5 and 10

Factors of 10x² that add up to 7x are 2x and 5x

that is:

2x × 5x = 10x²
2x + 5x = 7x