Topic Content:
- Elastic Collision
- Inelastic Collision
There are two types of collision namely elastic and inelastic.
Elastic Collision:
For elastic collision, the total momentum is conserved and the kinetic energyEnergy is the ability to do work. Energy exists in several forms such as heat, kinetic or mechanical energy, light, potential energy, and electrical energy. Units of Energy: The SI unit... More is also conserved.
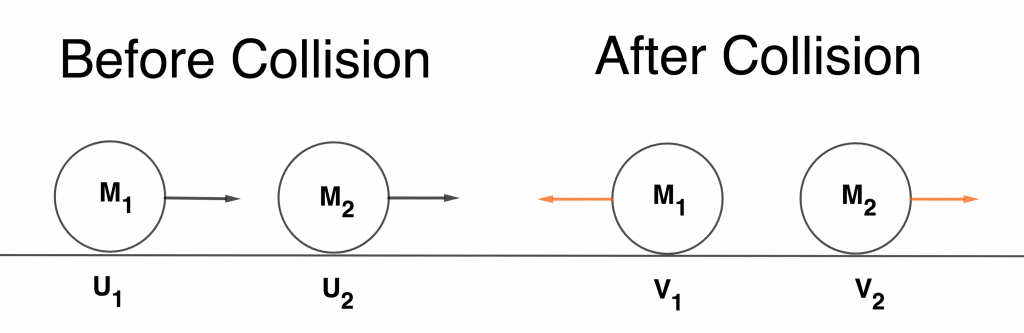
Let us put into consideration two masses m1 and m2 moving with initial velocities u1 and u2 before collision and with final velocities v1 and v2 in different directions after collision.
For a perfectly elastic collision, we can write an equation from the law of conservation of momentum and the law of conservation of kinetic energy.
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses