Energy of Simple Harmonic Motion

Summary:

When force and displacement are involved in SHM, energy or work done is also involved.

The system, at any instant of the motion, may contain some energy as Kinetic energy (K.E) or potential energy (P.E) or both.

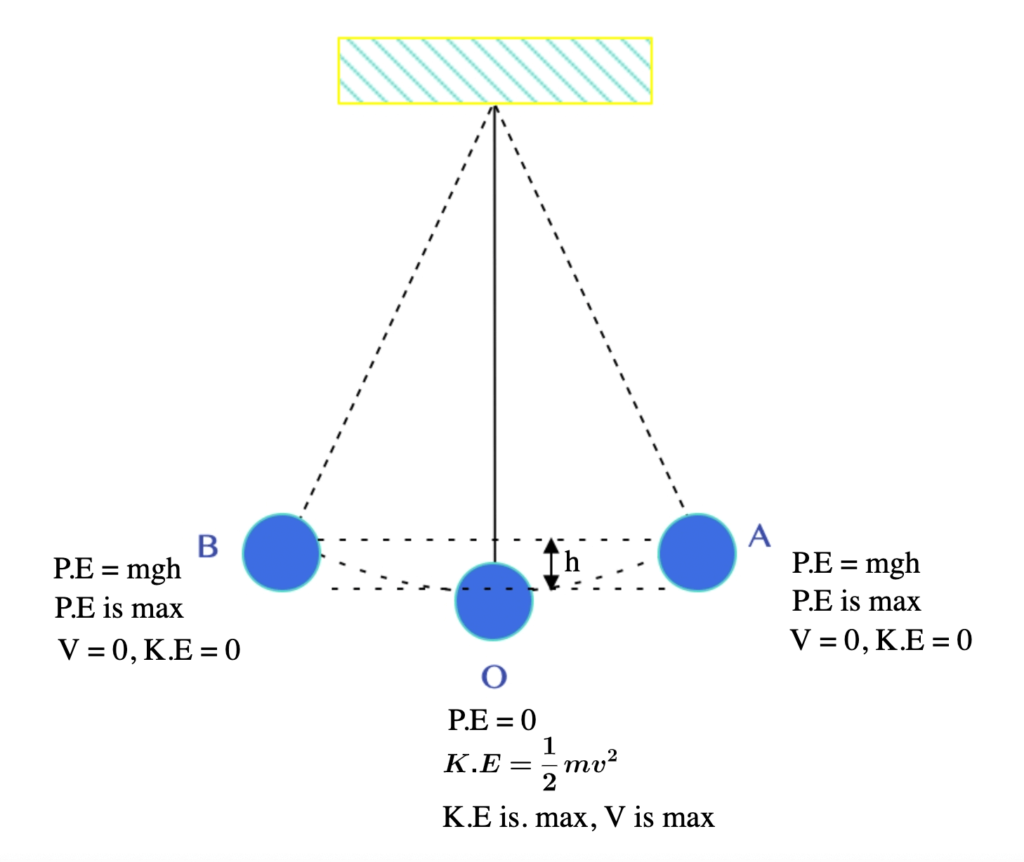
Consider the image above;

• The pendulum swings from the highest point through the centre of the swing to the other highest point.

• Let’s call the first highest point A, the centre O, and the other highest point B.

• The pendulum, swings from, A through, O to B

• At, point O, the Bob is at the lowest position, i.e height, h = 0, therefore the potential energy of the system is zero.

• Also at O, the speed of the pendulum, v_max is maximum and so the kinetic energy \( \left(\frac{1}{2} \scriptsize mv_{max}^2 \right)\) is maximum at this point.

• As the bob moves from O to B, the kinetic energy at O is gradually transformed to potential energy with the potential energy becoming maximum at B, which is at a height “h” above O

• At point B, the energy is potential energy and is equal to “mgh”. Where m is the mass of the bob, h is the height above the lowest level and g is the acceleration due to gravity.

• This is also the potential energy at “A” which is the same height above O, as B is.