Illustration of Simple Harmonic Motion

Mass on a String:

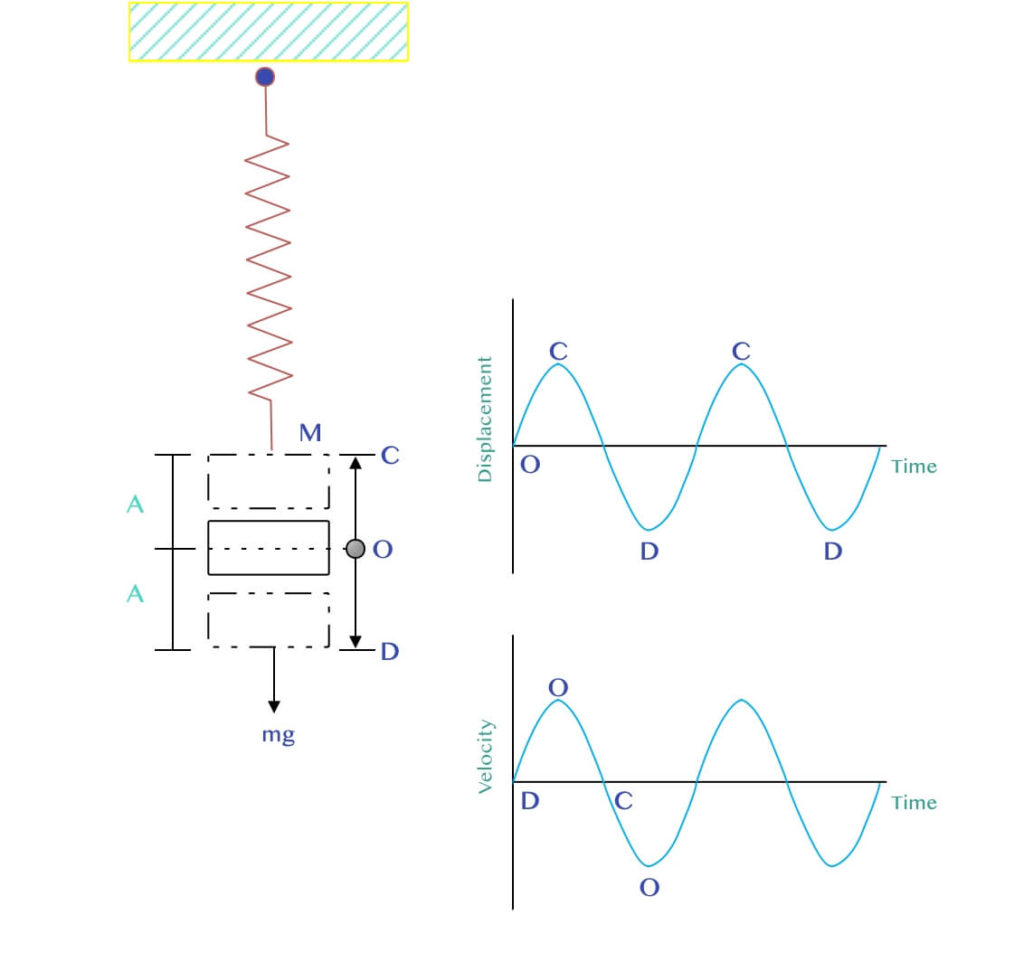
Let a mass M be hung from the lower end of a spring and the other end firmly clamped to a rigid support.

When the mass originally at position O (the equilibrium position) is pulled down to D and then released, it is observed, to move up and down in a regular pattern.

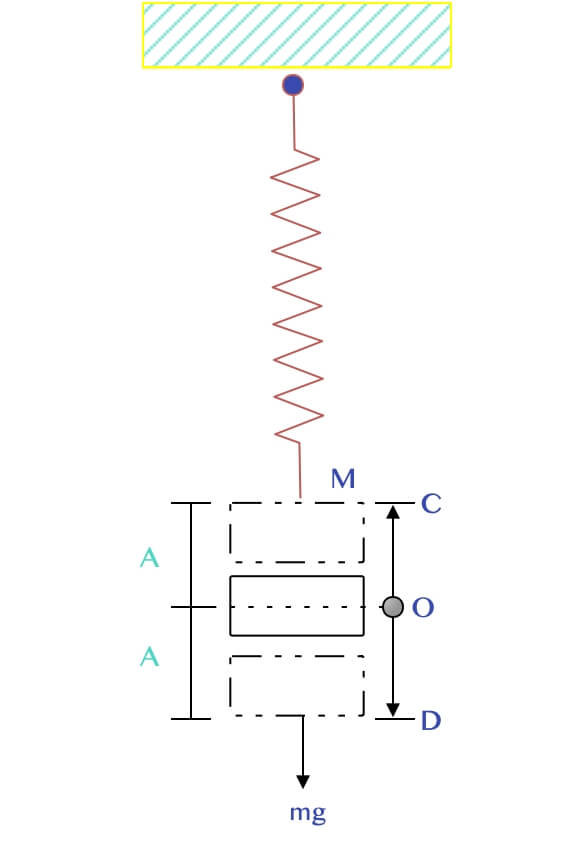
If the distance travelled on both sides of the equilibrium position is equal i.e. OD = OC, then the maximum displacement on either side of equilibrium are called the Amplitude of Oscillations.

Positive Amplitude – C
Equilibrium Position – O
Negative Amplitude – D

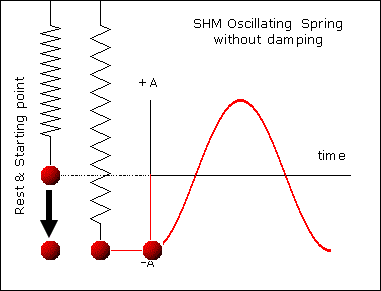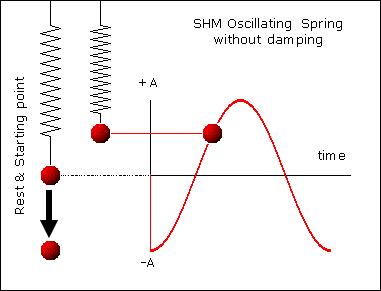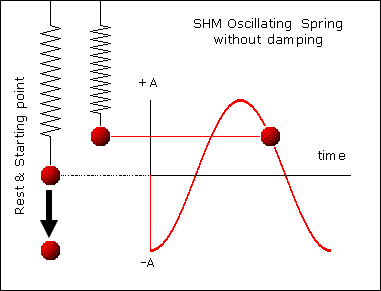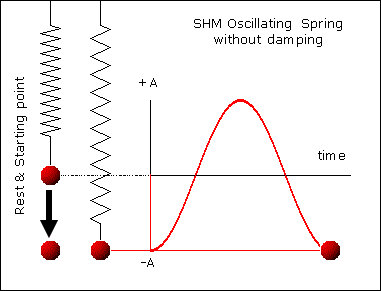
Using Hooke’s law, the restoring force, F, in the spring would be directly proportional to the extension, e, produced, provided the spring is not deformed.

F = -Ke

K is the spring constant.

Characteristics of Simple Harmonic Motion:

1. It is a periodic oscillatory motion about an equilibrium position.
2. The displacement is a sinusoidal function of time. It ranges from O to maximum displacement.
3. The velocity is maximum when displacement is O (equilibrium point).