Topic Content:
- Two or More Vectors Acting at a Point
When there are two or more vectors acting at a point, each of the vectors is resolved into the vertical and horizontal components.
After you have calculated the vertical component and the horizontal component of each vector, you then proceed to add all the vertical components to get a single vertical component. In a similar fashion, you are also to add all the horizontal components to get a single horizontal component.
The directions of the vectors must not be ignored. If the calculated vertical component is on the negative side of the y-axis, your calculated vertical component must be negative ( -ve / minus ). Also, if your calculated horizontal component is on the negative side of the x-axis, then your calculated horizontal component must be negative ( – ve / minus ).
This is shown below. Consider forces F1, F2, F3 and F4 acting at a point.
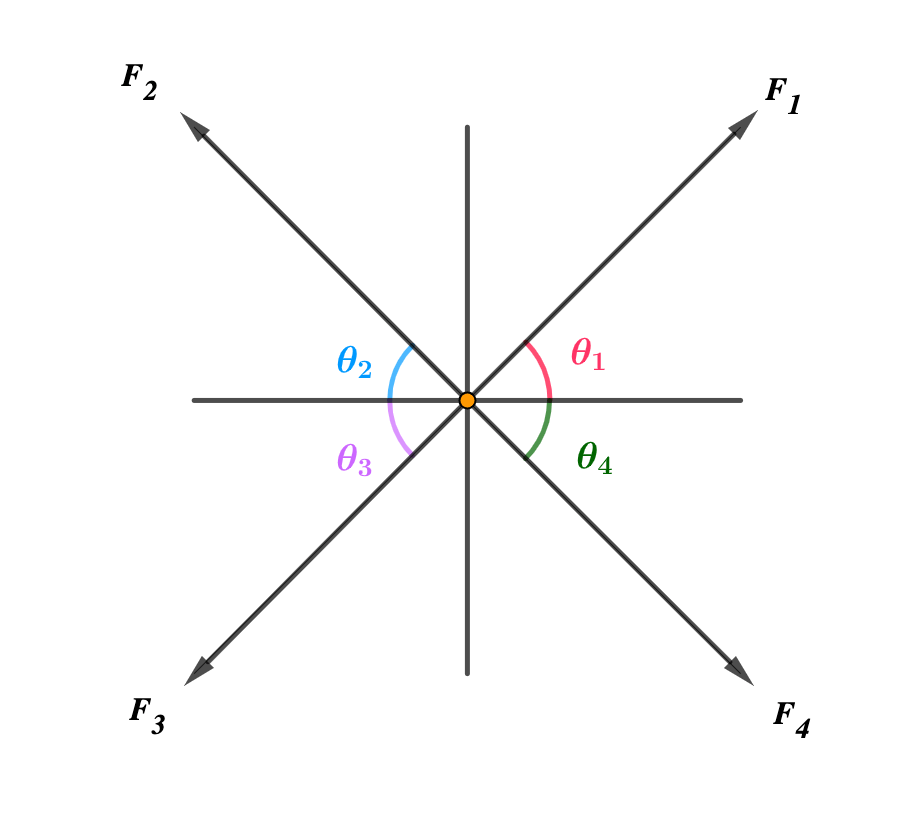
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses