Topic Content:
- Meaning of Scalar QuantityA scalar quantity is a quantity that does not depend on direction. It can also be defined as a quantity with magnitude only. Examples of Scalar Quantities include area, density, distance,... More
- Addition of Scalar Quantities
- Meaning of Vector QuantityVector quantities are quantities with magnitude and direction. Examples of vector quantities include displacement, velocity, position, force, and torque. More
- Representation of Vector
- Addition of Vector Quantities
What are Scalar Quantities?
Scalar quantities are physical quantities which have magnitude only or numerical value but no direction.
Examples of Scalar Quantities:
Examples of Scalar Quantities are:
- Mass
- Length
- DensityDensity is the measurement of how tightly a material is packed together i.e. how closely the particles are packed in the material. The tighter the material is packed the more its... More
- Time
- Distance
- Temperature
- Speed
- Volume
- Density
- Area
- Current
Addition of Scalar Quantities:
With scalar addition, all you have to do is add the values of each scalar item to obtain the total.
Examples of Addition of scalar Quantities:
• V1 + V2 = 10 cm3 + 30 cm3 = 40 cm3
• T1 + T2 = 273 K + 100 K = 373 K
• A1 + A2 = 200 m2 + 250 m2 = 450 m2
What are Vector Quantities?
Vector quantities are those quantities that have both magnitude and direction.
Examples of Vector Quantities:
Examples of Vector Quantities are
- Force
- Gravitational field
- Momentum
- Weight
- Velocity
- Acceleration due to gravity
- Magnetic field
- Electric field
- Displacement
- Acceleration
Representation of Vector:
A vector is always represented by a straight line with an arrow at one end pointing in a particular direction. The length of the line represents the magnitude of the vector, for example:

The vector \( \vec{\scriptsize AB} \) is 10 N in the Eastern direction.
Addition of Vector Quantities:
Example 1.1.1:
If two vectors \( \vec{\scriptsize B} \) and \( \vec{\scriptsize D} \) moved in the same direction and are 10 N and 12 N respectively, then, their resultant R is:
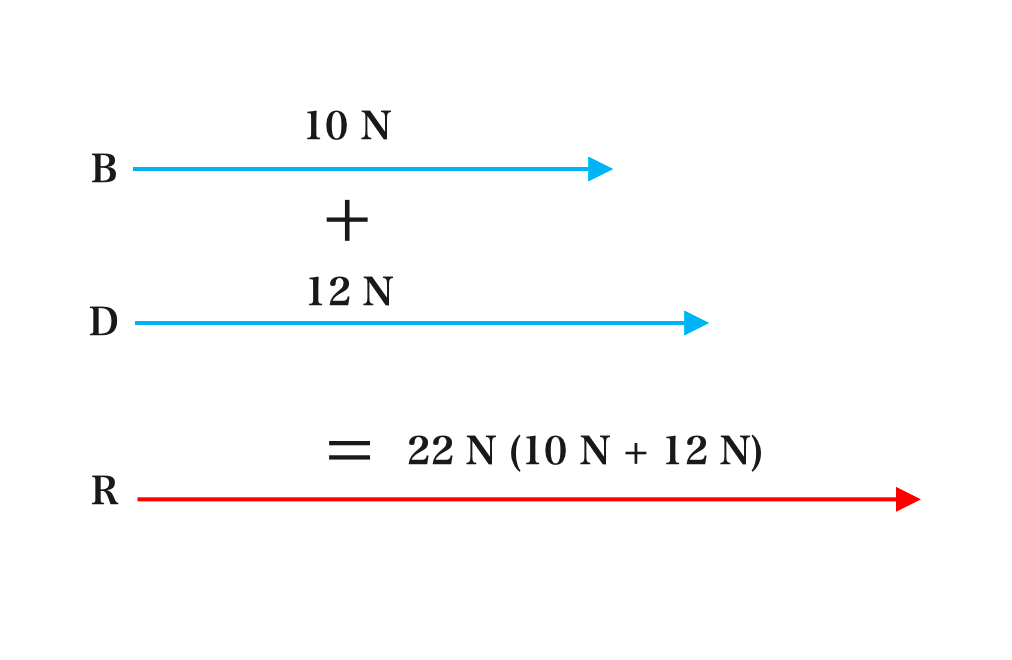
R = 22N
Example 1.1.2:
If \( \scriptsize \vec{B} \) and \( \scriptsize \vec{D} \) are in the opposite direction.
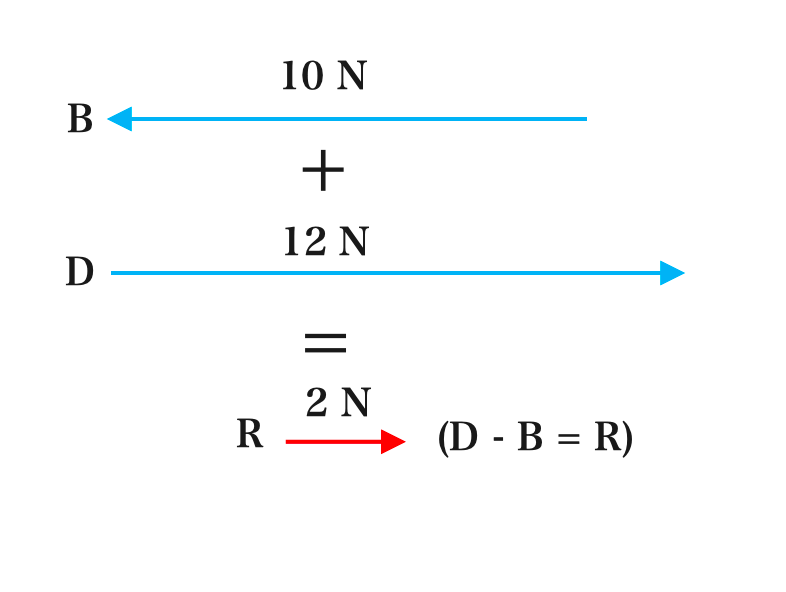
R = 2N
\( \scriptsize \vec{D} \: -\: \scriptsize \vec{B} = R \)The resultant is in the direction of the larger force i.e. \( \vec{\scriptsize D}\)
Example 1.1.3:
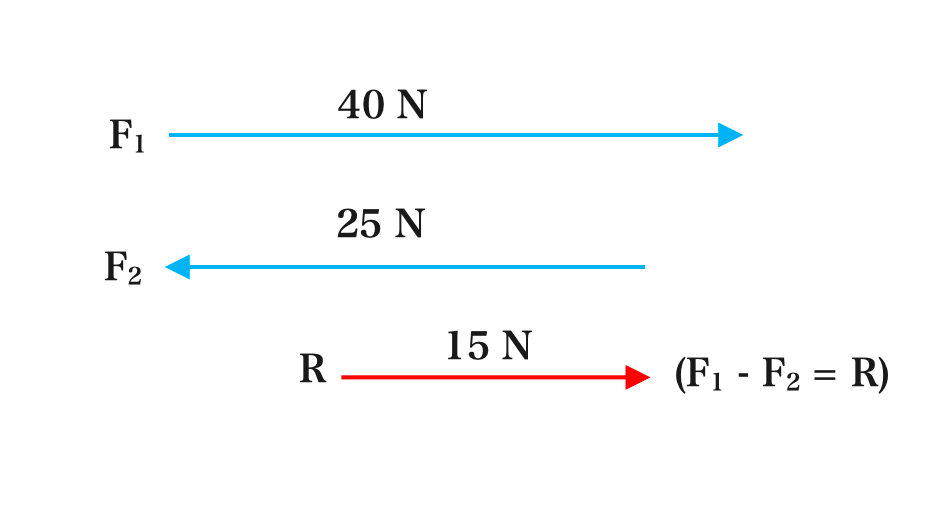
Given that 40 N force F1 travels from West to East and 25 N force F2 travels in the opposite direction to that of 40 N force. Find the resultant of the two vectors.
Solution:
Resultant Vector R = vector F1 + ( – vector F2)
Resultant vector R = vector F1 – vector F2
Resultant vector R = 40 N – 25 N = 15 N
Example 1.1.4:
90 N force travelled from east to west. If 35 N travelled in a direction that is opposite to that of 90 N, what is the force?
Solution:
Let 90 N be F1 and 35 N be F2
East to West is a negative direction of travel, therefore F1 = – 90 N
35 N travelled in the opposite direction to 90 N,
therefore F2 = + 35 N
Resultant vector R = – vector F1 + vector F2
Resultant vector R = – 90N + 35N = – 55N
Example 1.1.5:
Two vectors of equal magnitude that are pointing in opposite directions will sum to zero. \( \scriptsize \vec{B} \: – \: \scriptsize \vec{D} = 0\)

R = 0.
Example 1.1.6:
In the vector diagram below, find the resultant and direction of the two vectors.
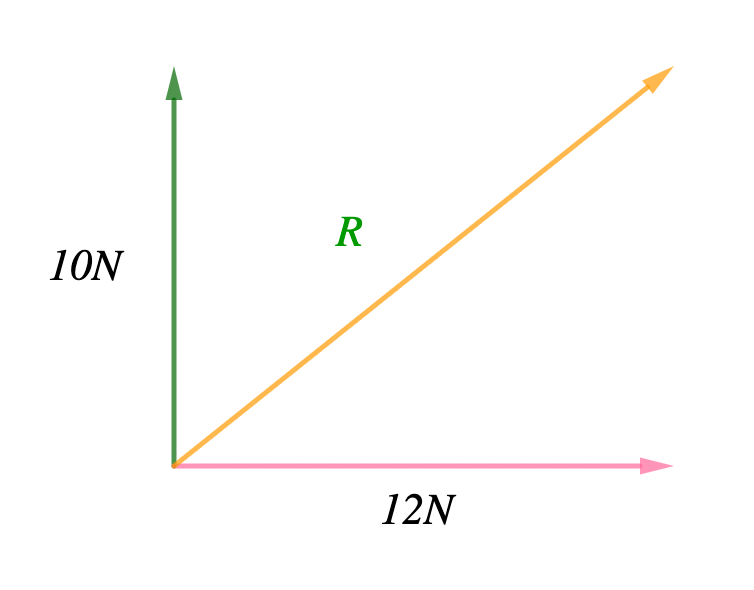
Solution:
(i) When two vectors are inclined at 90° (perpendicular) to each other, their resultant is obtained using the Pythagoras theorem.
The resultant of the vectors is represented by the hypotenuse of the triangle in such a way that the direction of the resultant vector is opposite to the direction of the two vectors. The length of the hypotenuse represents the magnitude/size of the resultant vector.
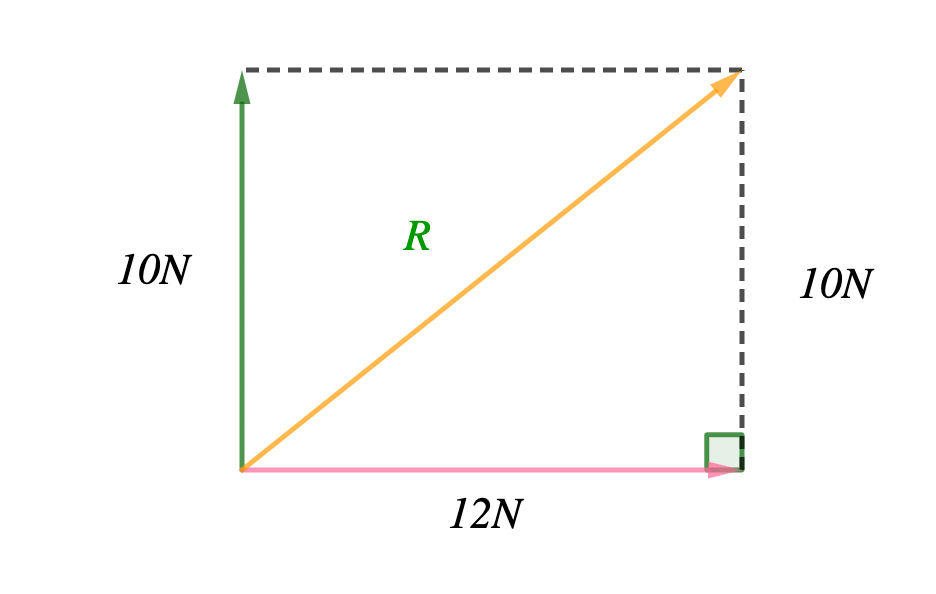
Using Pythagoras,
(i)
R2 = 102 + 122
R2 = 100 + 144
R2 = 244
R = \( \scriptsize \sqrt{244} \)
= 15.6 N
(ii) The direction is given by
\( \scriptsize tan \: \theta = \normalsize \frac{opp}{adj} = \frac{10}{12} \) \( \scriptsize tan \: \theta = 0.833\)θ = tan-1 (0.833) = \( \scriptsize 39.8^{\circ} \)
The resultant can also be found by scale drawing.
The resultant vector is a single vector which would have the same effect in magnitude and direction as the original vectors acting together.



This was so cool it actually matched with what I learnt at school
This is fantastic,it just like I am in class again
This is awesome it’s helps for quick understanding
I so enjoy this website
This is lovely! A good progression from easy to complex
I really enjoyed the note. It explicit and the content is valid. Thanks for also making it free.
I love this