Topic Content:
- Types of Polygons
- Interior Angles of a Polygon
- Exterior Angles of a Polygon
We have other types of polygons aside from triangles and quadrilaterals.
Examples are
| Polygon | Number of sides |
| Pentagon | 5 sides |
| Hexagon | 6 sides |
| Heptagon | 7 sides |
| Octagon | 8 sides |
| Nonagon | 9 sides |
| Decagon | 10 sides |
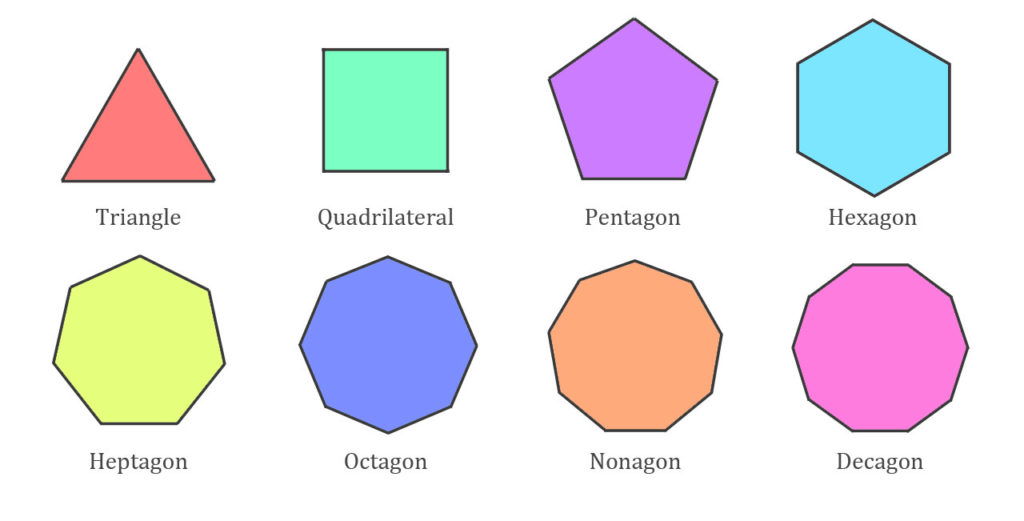
Types of Polygons:
Regular Polygon: A regular polygon is a polygon with its sides and angles equal.
Irregular Polygon: These are polygons with unequal lengths of sides and angles.
Convex: A convex polygon has all its interior angles either acute or obtuse i.e less than 180°.
Concave Polygon: In a concave polygon at least one of its interior angles is reflex.
Interior Angles of a Polygon:
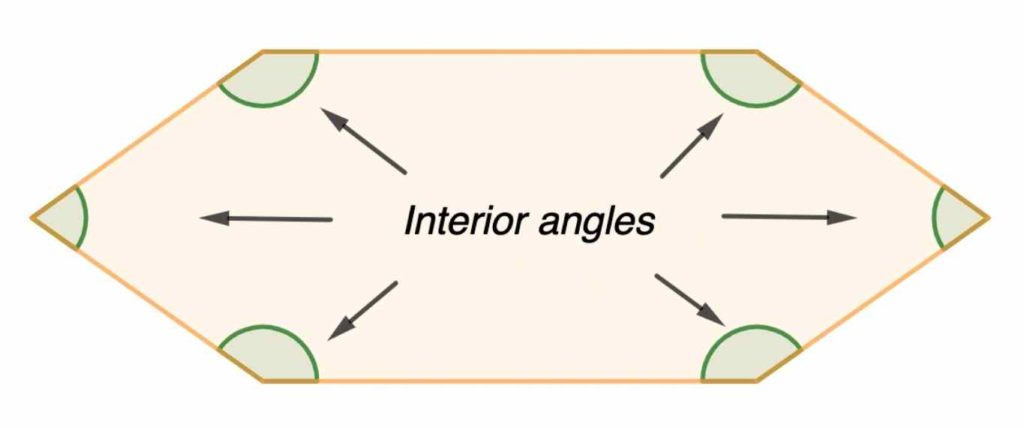
The interior angles of a polygon are the angles inside the polygon. A polygon has the same number of sides as the number of angles inside it.
Formulae:
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses