Topic Content:
- Meaning of Linear Inequalities
- Number Line
- Showing Inequalities on a Number Line
Inequalities are said to be linear if they have no square or higher powers of the unknown. In other words, the highest power of the unknown is 1.
For example:
\( \scriptsize 2x > 10 \) \( \scriptsize 4x \: – \: 5y > \: -18 \)Number Line:
A number line is a visual representation of a set of real numbers as a series of points.
Showing Inequalities on a Number Line:
On a number line, you can show inequality by obeying these rules.
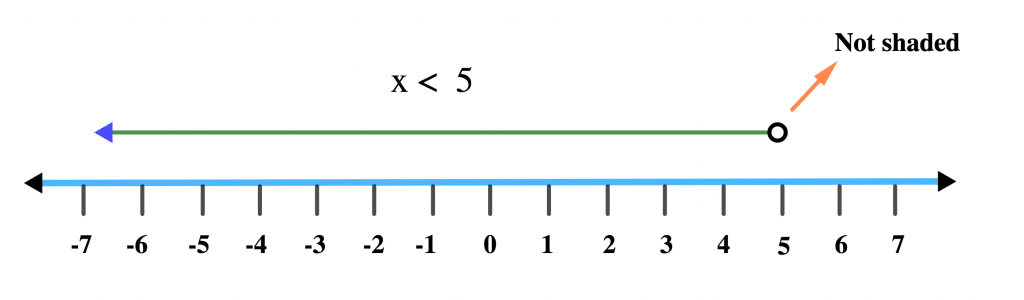
For ‘<’ the arrow points to the left, but the starting point is not shaded.
For Example, x < 5 is drawn this way
For ‘>’, the arrow points to the right and the starting point is not shaded.
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses