Combining the Velocity-Time Graphs

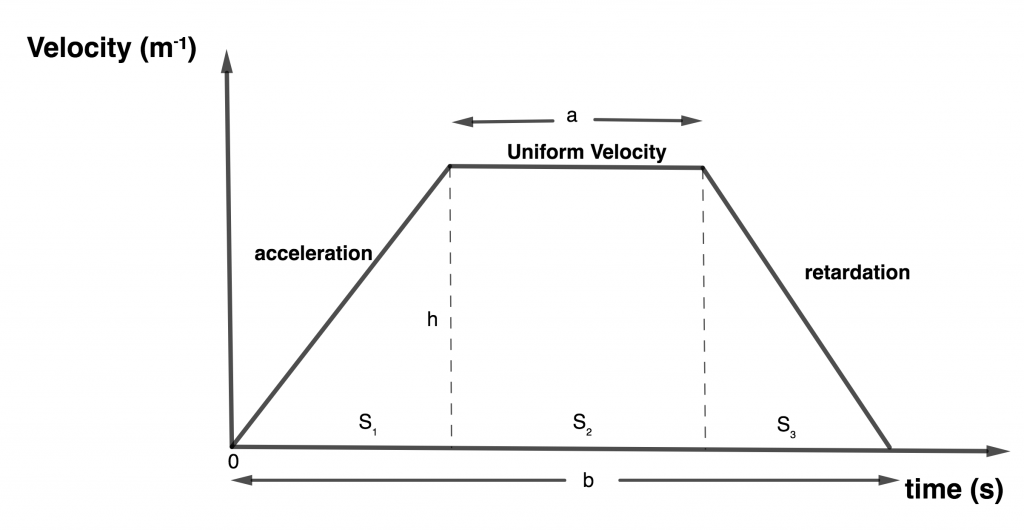
The total distance travelled is the total area under the graph from the graph, the shape is that of a trapezium.

 ∴ Total distance covered = Area of a trapezium

=   \( \frac{1}{2}\)(Sum of parallel sides) x h

=   \( \frac{1}{2} \scriptsize (a \: + \: b) \: \times \: h\)

Also, breaking the graph into components, S_1, S_2, S₃

S₁ is a right angle triangle = distance covered = Area of a right angle triangle

S₁ = \( \frac{1}{2} \scriptsize \: \times \: base \: \times \: height \\ = \frac{1}{2} \scriptsize bh\)  

S₂ = Area of a rectangle = total distance covered = L x b

S₃ = Area of a right angle triangle = \( \frac{1}{2} \scriptsize \: \times \: base \: \: \times \: height \\ =\frac{1}{2} \scriptsize bh \)

 ∴ the total distance covered = S₁ + S₂ + S₃